基础知识
MATLAB系统环境
如果一个命令很长,可以在第一行最后加上三个点,按下回车在下一行继续输入。这三个点称为续行符
1
2>> s=1-1/2+1/3-1/4+1/5...
1/6+1/7选择当前文件夹,可以手动选择,也可以在命令行窗口中使用cd命令进入
MATLAB的搜索路径

MATLAB的搜索路径

MATLAB数值数据
数值数据类型
整形
- 无符号整数:8位(0 ~ 28-1)、16位、32位、64位
- 带符号整数:8位(-27 ~ 27-1)、16位、32位、64位
- uint函数将数值数据转换为无符号8位整数。int8函数将数值数据转换为带符号8位整数
浮点型(MATLAB中默认是双精度)
- 单精度(4字节):
- 双精度(8字节):
- single函数:将其他类型的数据转换为单精度型
- double函数:将其他数据类型转换为双精度型
复数型
包含实部和虚部两个部分,实部和虚部默认为双精度型,虚部单位用i或者j表示
- real函数:求复数的实部
- imag函数:求复数的虚部
数值数据的输出格式
format命令(只是影响数据输出格式,不影响数据的计算和存储)
用法:
format 格式符1
2
3
4
5
6
7
8#例子
>> format long
>> 50 / 3
ans =
16.666666666666668
>> format #回到默认输出格式,short格式
>> 53 / 3
ans = 16.6667
常用数学函数
函数的调用格式为:
函数名(函数自变量的值)函数的自变量规定为矩阵变量,当然也可以是标量,标量本身是矩阵的一种特例。函数在运算时是将函数逐项作用于矩阵的每个元素上,所以最后运算的结果就是一个与自变量同型的矩阵


常用函数的应用
三角函数有以弧度为单位的函数和以角度为单位的函数。如果是以角度为单位的函数就在函数名后加“d”。
1
2
3
4
5
6>>sin(pi/2)
ans =
1
>>sind(90)
ans =
1abs函数可以求实数的绝对值、复数的模、字符串的ASCII的码值
1
2
3
4
5
6
7
8
9>>abs(-4)
ans =
4
>>abs(3+4i)
ans =
5
>>abs('a')
ans =
97用于取整的函数
- round:按照四舍五入进行取整
- fix:舍去小数取整
- floor:向下取整
- ceil:向上取整
一些数值处理函数
rem函数:
1
2
3
4
5#求345除以10的余数
>> m=345;
>> m1 = rem(m,10)
m1 =
5isprime()函数:判断传入的数是否是素数,返回1就是素数
find函数用于寻找k矩阵中所有的非零的数。k1向量中的元素为k向量中非零元素的序号,即x中素数元素的序号


变量及其操作
变量基本知识
- 变量的本质上是内存单元的一个抽象
- 在MATLAB中,变量名以字母开头、后接字母、数字或下划线的字符序列,最多63个字符
- MATLAB中区分字母的大小写
- 标准函数名及命令名必须用小写字母
预定义变量
- ans是默认复制变量
- i和j表示虚数单位
- pi代表圆周率
- NaN代表非数
变量的管理
通过工作区删除和操作
who和whos命令查看变量清单。who只给出名称,whos会给出详细信息
内存变量文件:用于保存MATLAB工作区变量的文件叫做内存变量文件。扩展名为.mat,也叫MAT文件
save命令:创建内存变量文件load命令:装入内存变量文件1
2
3>>save mydata a x # 将变量a和x保存在mydata文件中
>>load mydata #将mydata中的变量装入工作区
MATLAB矩阵的表示
矩阵的建立
直接输入建立矩阵
1
2
3
4
5>> A = [1,2,3; 4,5,6; 7,8,9]
A =
1 2 3
4 5 6
7 8 9利用建好的矩阵建立更大的矩阵
1
2#假设已知AB为矩阵
>> c = [A,B; B,A] #建立c矩阵冒号表达式
格式:
e1:e2:e3:e1是初始值,e2是步长,e3是终止值1
2
3>>t = 1:1:5
t =
0 1 2 3 4 5省略步长则默认为1
linspace函数:
- 格式:
linspace(a,b,n):其中a表示生成向量的第一个元素,b是生成向量的最后一个函数,n是元素总数,当n省略时,自动生成100个
- 格式:
可以用实部矩阵和虚部矩阵构成复数矩阵

结构矩阵和单元矩阵
结构矩阵
格式:
结构矩阵元素.成员名=表达式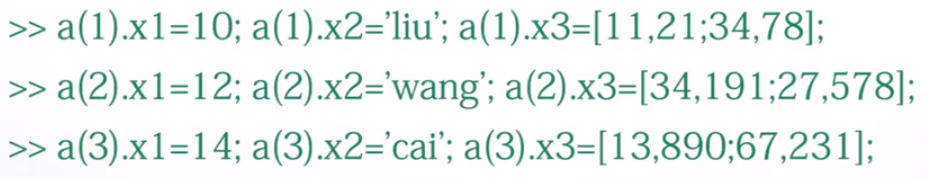
单元矩阵
建立单元矩阵和一般矩阵相似,直接输入就可以了。只是单元矩阵元素用打括号扩起来

矩阵元素的引用
矩阵元素访问
通过下标引用
当给出的下标大于矩阵本身,会自动扩展矩阵。没有赋值的直接符赋零

通过序号引用:在MATLAB中,矩阵元素按照列存储。所以矩阵元素的序号就是其排列顺序号。
sub2ind函数:将矩阵中指定元素的行、列下标转换为储存的序列号。调用格式为

ind2sub函数

利用冒号表达式获取子矩阵
子矩阵是指由矩阵的一部分元素构成的矩阵

end运算符

删除矩阵元素
利用空矩阵删除矩阵元素

改变矩阵形状
reshape函数
用法:
reshape(A,m,n):在矩阵总元素不变的前提下,将矩阵A从新排成m×x的二位矩阵注意:该函数只改变原矩阵的行数和列数,并不改变原矩阵元素个数及其存储顺序
A(:):将矩阵A的每一列元素堆叠起来,成为一个列向量
MATLAB基本运算
算术运算
基本算数运算
基本算数运算符:+(加)、-(减)、*(乘)、/(右除)、\(左乘)、^(乘方)
- matlab的算数运算是在矩阵意义下进行的
- 单个数据的算数运算只是矩阵运算的一种 特例
如果A矩阵是非奇异方阵,则B/A等效于Binv(A),A\B等效与inv(A)\B

点运算
兩矩阵进行点运算是指他们的对应元素进行相关的运算,要求兩矩阵同型
.*./.\.^
关系运算
- 当参与比较的量是两个同行的矩阵时,比较的是对矩阵相同位置的元素,按标量关系运算规则逐个进行。最终的关系运算的结果是一个与原矩阵同型的矩阵,它的元素由0和1构成
- 当参与比较的是一个是标量,而另一个是矩阵时,咋把标量与矩阵的每一个元素按标量关系运算规则逐个比较,最终关系运算的结果是一个与原矩阵相同型的矩阵,他的元素由零或一构成
<(小于)
<=(小于等于)
>(大于)
>=(大于等于)
==(等于)
~=(不等于)

逻辑运算
- &(与)
- |(或)
- ~(非)
- 若参与逻辑运算的是两个同型矩阵,那么将对矩阵相同位置上的元素按标量规则逐个进行运算,最终运算结果是一个与原矩阵同行的矩阵,其元素由0和1构成
- 若参与逻辑运算的一个是标量,一个是矩阵,那么将在标量与矩阵中的每个元素之间,按标量规则,逐个进行运算,最终运算结果是一个与原矩阵同型的矩阵,其元素由0和1构成
矩阵处理
特殊矩阵
通用特殊矩阵
zeros函数:产生全0矩阵,即零矩阵ones函数:产生全1矩阵,即幺矩阵eye函数:产生对角线矩阵。当矩阵呢是方阵时,得到一个单位矩阵rand函数:产生(0,1)区间均匀分布的随机矩阵(不包括0和1)randn函数:产生均值为0,方差为1的标准正态分布随机矩阵
调用格式
zeros(m):产生m×m零矩阵zeros(m,n):产生m×n零矩阵zeros(size(A)):产生与矩阵A同样大小的零矩阵
特殊矩阵
魔方矩阵
- 用法:
magic(n) - n阶魔方阵由1,2,3,4….n2,共n2个数组成。且每行每列以及主、副对角线上各n个元素之和都相等
- n阶魔方阵每行每列元素的和为(1+2+3+…+n2)/n = (n + n3) / 2
- 该函数产生一个特定的魔方阵
- 用法:
范德蒙矩阵
- vander(n)
希尔伯特矩阵
- 用法:
bilb(n) - 第i行第j列的元素为1/(i+j-1)
- 用法:
帕斯卡矩阵
- 用法:
pascal(n) 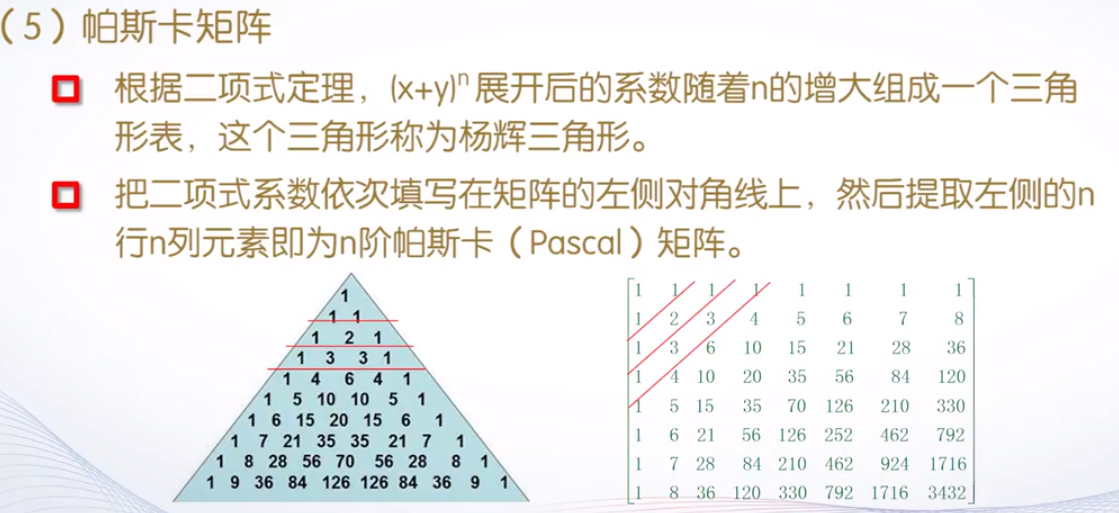

- 用法:
伴随矩阵
用法:
compan(p)。这里的p是一个多多项式的系数向量,高次幂*在前低次幂在后什么是伴随矩阵:

实例:

矩阵变换
对角阵
- 定义
- 对角矩阵:只有对角线上由非零元素的矩阵
- 数量矩阵:对角线上的元素相等的矩阵
- 单位矩阵:对角线上的元素都为一的对角矩阵
- 提取对角线的元素
diag(A):提取主对角线元素,产生一个列向量diag(A,k):提取矩阵A第K条对角线的元素,产生一个列向量
- 构造对角阵
diag(v):以向量V为主对角线元素,产生对角矩阵diag(v,k):以向量v为第k条对角线元素,产生对角矩阵
三角阵
矩阵的转置
矩阵的旋转
矩阵的翻转
矩阵求逆
矩阵求值
矩阵的特征与特征向量
程序流程控制
文件相关
分为脚本文件和函数文件
创建脚本文件可以手动点击创建
创建脚本可以使用命令
edit ×××。例:>>edit test(即创建文件名为test的脚本文件)建立函数文件使用
function关键字
一些基本命令
- 数据的输出:
disp(输出项):输出项可以使字符串,也可以是矩阵等 - 程序的暂停:
pause(延迟秒数):如果不输入秒数,则会停止等待用户输入任意键继续
if、swith、for、while
if
当条件结果为标量时,非零表示条件成立。零表示不成立
当条件结果为矩阵时,如果矩阵非空,且不含零元素,则条件成立,否则不成立
单分支语句
1
2
3if 条件
语句组
end双分支
1
2
3
4
5if 条件
语句组
else
语句组
end多分支
1
2
3
4
5
6
7
8
9
10if 条件1
语句组
elseif 条件2
语句组
......
elseif 条件n
语句组
else
语句组
end
swich
1
2
3
4
5
6
7
8
9switch 表达式1
case 结果集1 #这里之所以叫结果集,是因为可以`case {1,2,3}`这样写
语句组
case 结果集2
语句组
.....
otherwise
语句组
endnum2cell函数可以将数值向量转化为单元数据。例如case num2cell(0:34)就表示{0~34的整数}
for
1
2
3
4
5
6
7
81
for 循环变量=表达式1:表达式2:表达式3 #例:for k=1:2:10
循环体
end
2
for k=矩阵表达式 #例:for k=[1,2,3]。如果是一个多行一列的矩阵,for只执行一次
end
while
1
2
3while 条件
循环条件
end
break 和 continue
函数文件的定义与调用
函数文件基本结构
1
2function 输出形参表=函数名(输入形参表)
函数体语句当有多个形参时,形参之间用逗号隔开,形成形参表。当输出形参多余一个时,应用方括号扩起来,形成一个输出矩阵
return会打断函数的运行
调用格式:
[输出实参表]=函数名(输入实参)匿名函数
基本格式:
函数句柄变量=@(匿名函数输入参数)匿名函数表达式例子
1
2
3
4
5
6>> f=@(x,y) x^2+y^2
f =
@(x,y)x^2 + y^2
>> f(3,4)
ans =
25还可以给已经存在的函数定义句柄:格式:
函数句柄变量=@函数名(自定义函数或者内部函数)
函数参数与变量
参数的可调性
nargin:记录了输入实参的个数nargout:记录了输出实参的个数全局变量
定义格式:
global 变量名
局部变量:直接定义即可
绘图
二维曲线
plot函数调用格式:
plot(x,y)最简单的调用格式:
plot(x):画出来的图形,横坐标是x的下表,纵坐标是值。当plot函数的参数是复数向量时,则分别以该向量元素实部和虚部为横、纵坐标绘制出一条曲线plot(x,y)参数的变化形式
- 如果矩阵y的列数等于x的长度,则以向量x为横坐标以外的每个行向量为纵坐标,绘制曲线曲线的条数等于y的行数
- 如果矩阵y的行数等于x的长度,则以向量x为横坐标,以y的每个列向量为纵坐标绘制曲线,曲线的条数等于y的列数
- 当x、y是同型矩阵时:以x、y对应列元素为横、纵坐标分别绘制曲线,曲线的条数等于矩阵的列数
含多个输入参数的plot函数:
plot(x1,y1,x2,y2....,xn,yn):其中,每一向量对构成一组数据点的横、纵坐标,绘制一条曲线含选项的plot函数:plot(x,y,选项)
线性(默认实线)
-:实线::虚线-.:点画线--:双画线
颜色(自动循环使用颜色)
r:红色g:绿色b:蓝色w:白色k:黑色- ….
数据标点(默认无)
*:星号O:圆圈S:方块P:五角星^:朝上的三角符号- ….
例子
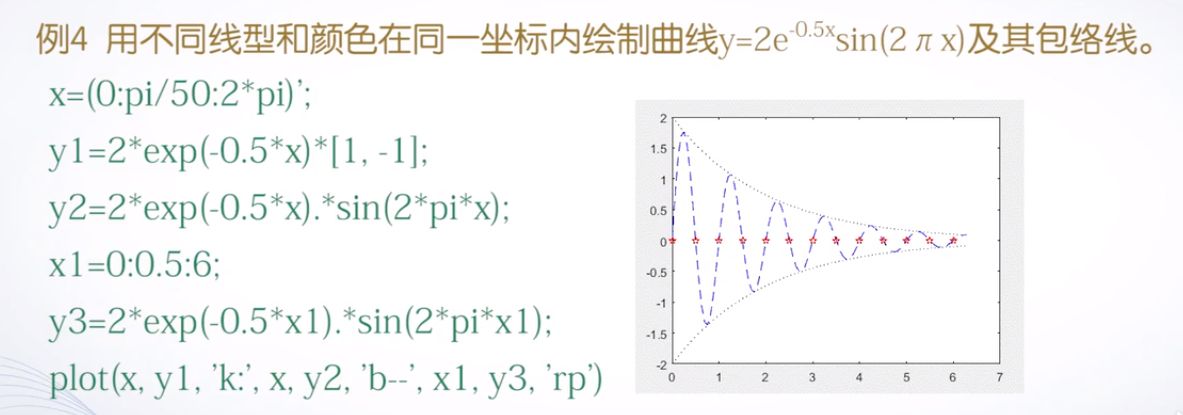
fplot函数:可根据参数函数的变化特性,自适应设置间隔- 调用格式:
fplot(f,lims,选项):其中f代表一个函数,通常采用函数句柄的形式。lims为x轴的取值范围,采用二元向量[xmin,xmax]描述,默认值为[-5,5]。选项定义与plot函数相同(不建议绘制点,容易导致图形变形) - 双输入函数参数的用法:
fplot(funx,funy,tlims,选项):其中funx、funy代表函数,通常采用函数句柄的形式。tlims为参数函数funx和funy的自变量的取值范围,用二元向量[tmin,tmax]描述
- 调用格式:
绘制图形的辅助操作
给图形添加标注
titlt(‘图形标题’)如果有多行标题显示,可以使用
title({‘标题一’,‘标题二’}),会列向显示在图形标题中使用LaTex格式控制符

含属性设置的title函数
用法:
title(图形标题,属性名,属性值)
xlabel(‘x轴说明’)、ylabel(‘y轴说明’)text(x,y,‘图形说明’)、gtext(‘说明’)- text函数还可以加上箭头之类的
- gtext函数,十字光标跟随鼠标移动。单击,即可放置文本
legend(图例1,图例2,....)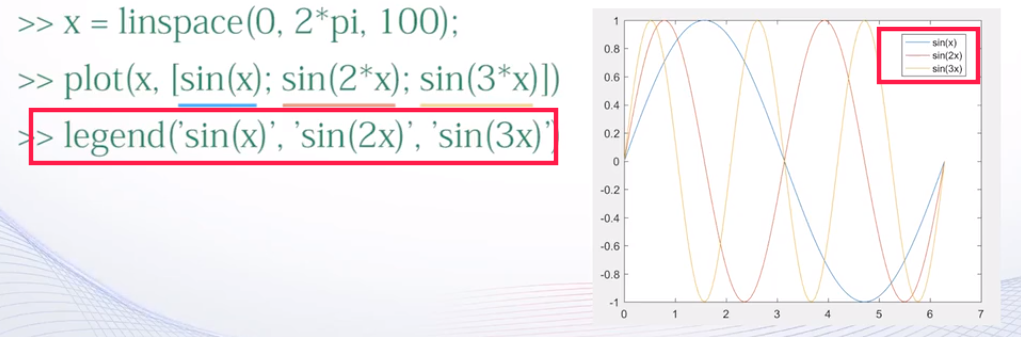
坐标控制
axis函数:一般来说MATLAB会自动规定坐标轴范围,手动规定只是为了一些特殊情况用法:
axis([xmin,xmax,ymin,ymax,zmin,zmax])。也可以只给出前四个参数其他用法

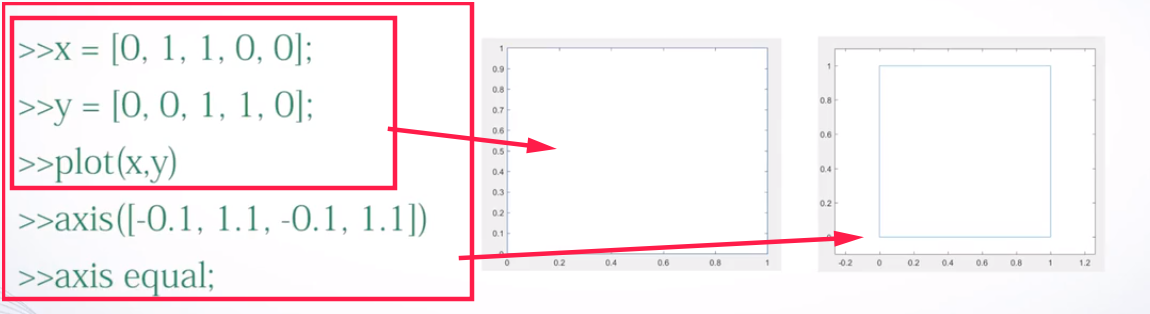
给坐标系加网格线
grid on:给坐标系加上网格线grid off:取消网格线grid:用于在前两种格式进行转换
给图形加边框(默认有边框)
box on:控制保持原有图形box off:控制刷新图形窗口box:在两种状态之间转换
图形保持
可在一个图形上继续叠加新的图形
hold onhold offhold
图形窗口的分割
子图:同一图形窗口中的不同坐标系下的图形称为子图
subplot(m,n,p):其中m和n表示将图形窗口分成m×n个绘制区,p指定当前活动区- 实例:
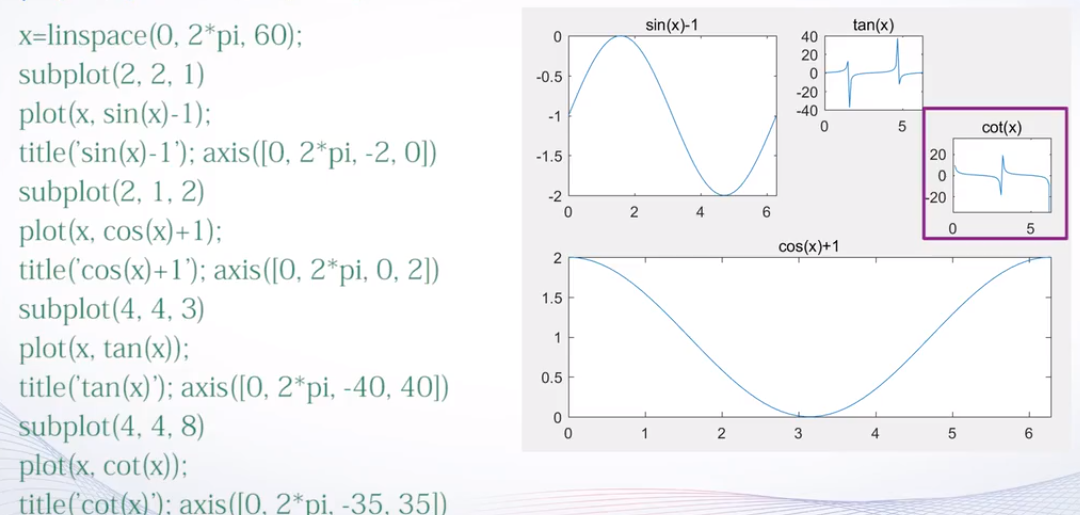
其他形式的二维图形
对数坐标图(选项与plot函数一致)
semilogx(x1, y1, 选项1, x2, y2, 选项2, ...):半对数坐标,x为为常用对数刻都semilogy(x1, y1, 选项1, x2, y2, 选项2, ...):半对数坐标,y为为常用对数刻都loglog(x1, y1, 选项1, x2, y2, 选项2, ...):全对数坐标
极坐标图
- 用法:
polar(theta, rho, 选项):theta为极角, rho为极径,选项与plot函数相同
- 用法:
统计图
条形类图
条形图
bar函数:绘制垂直条形图
调用格式:
bar(y,style):其中y是数据(如果y是向量,则下标作为横坐标。如果y是矩阵,则行号作为横坐标,分组绘制矩形条)选项style用于指定分组排列模式:
"grouped":簇状分组,"stacked":堆积分组调用格式:
bar(x,y,style):x是横坐标,y是数据。x是向量,y可以是矩阵,向量长度等于y的列数
barh函数:绘制水平条形图。
用法与bar类似
直方图
hist函数:用于绘制直角坐标系下的直方图- 调用格式1:
hist(y):通常y是向量。将向量y中最大值和最小值之间的区间等分。并统计落在每个区间的个数据个数,然后以数据个数为高度绘制图形(默认是10个区间) - 调用格式2:
hist(x,y):x用于指定划分方式,若x是标量,则划分为x个区间,若向量x中的每一个数指定分组的中心值,x元素的个数等于区间数
- 调用格式1:
rose函数:用于绘制极坐标系下的直方图调用格式:
rose(theta,x):theta是一个向量,用于确定每一区间与原点的角度,选项x用于指定区间的划分方式。绘图是将圆划分成若干个角度相同的扇形区域,每一个扇形区域三角形的高度反应落入该区间的的theta元素的个数,若x是标量,则在0到2pi区间内均匀划分成x个扇形区域。x缺省时,默认按20个区间等分例子

饼图
pie函数- 调用格式:
pie(x,explode):x存储待统计数据(通常x为向量,x的每个元素对应一个扇形,每个扇形对应的角度反映对应x元素在整体所占的比重),选项explode控制图形块的显示模式,与explode的非零值对应的部分将从饼图中心分离出来。explode是与x同等大小的向量,省略explode时,饼图是一个整体
- 调用格式:
area函数
类比plot函数
散点图
- scatter函数:散点图
- 调用格式:
scatter(x,y,选项,‘filled’):参数x、y用于定位数据点,选项参考plot函数。如果数据点标记是封闭图形(如:圆圈、方块),可以指定filled填充标记,省略时,数据点是空心的
- 调用格式:
- stairs函数:阶梯图
- stem函数:杆图
- scatter函数:散点图
矢量类图形()
compass函数:罗盘图
feather函数:羽毛图
quiver函数:箭头图
调用格式:
quiver(x,y,u,v),其中(x,y)指定矢量起点,(u,v)指定向量终点
三维曲线
- plot3函数
- 调用格式:
plot3(x,y,z):其中x,y,z组成一组曲线的坐标 - 一般x y z同型
- 当x y z是同型矩阵时,以对应的列元素组成一组曲线。
- 参数x y z中有向量也有矩阵时,向量的长度应与矩阵相符(行向量的长度与矩阵的列数相同,列向量的长度与矩阵的行数相同)
- 也可以多组输入,同时绘画:
plot3(x1, y1, z1, x2, y2, z2.....)每一组x,y,z向量构成一组数据点的坐标,绘制一条曲线 - 也可以加上选项,参考plot的选项:
plot3(x,y,z,选项)
- 调用格式:
- fplot3函数
- 若x,y,z坐标用参数方程定义,且只有一个自变量可以使用fplot3函数
- 基本调用格式:
fplot3(funx,funy,funz,tlims):其中funx、funy、funz代表曲线x、y、z坐标的函数,通常采用函数句柄的形式。tlims为参数函数自变量的取值范围,采用二元向量[tmin,tmax]描述,默认为[-5, 5]
三维曲面
平面网格数据的生成
- 利用矩阵运算生成
- 利用meshgrid函数生成
- 调用格式:
[X,Y]=meshgrid(x,y):其中,x、y为向量,存储网格点坐标的X、Y为矩阵
- 调用格式:
绘制三维曲面的mesh函数和surf函数
mesh函数用于绘制三维网格图
- 调用格式:
mesh(x,y,z,c):一般xyz是同型矩阵。其中x、y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定不同高度下的曲面颜色。c省略时,c等于z - 其他调用格式:
mesh(z,c):当xy省略时,z矩阵的第二维下标当作x轴坐标,z矩阵的第一维下标当作y轴坐标
- 调用格式:
surf用于绘制三维曲面图
- 调用格式:
surf(x,y,z,c) - 与mesh类似
- 调用格式:
带等高线的三维网格曲面函数meshc
带底座的三维网格曲面函数meshz
具有等高线的曲面函数surfc
具有光照效果的曲面函数surfl
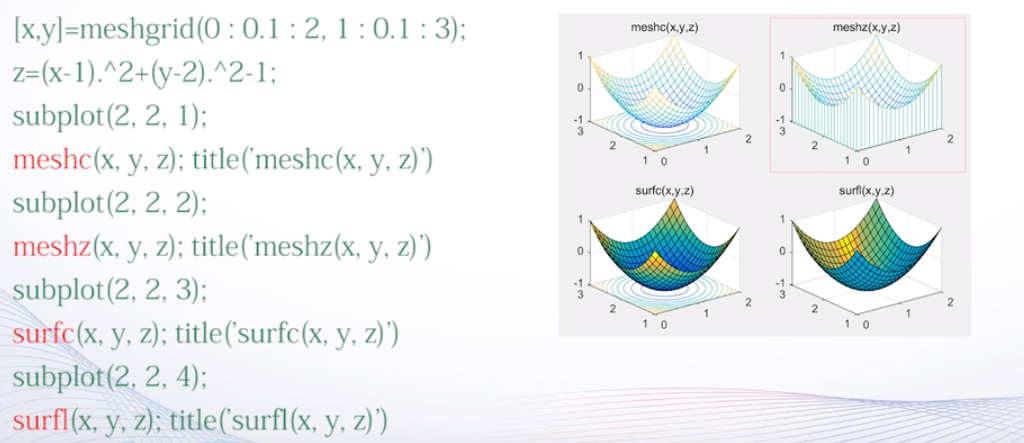
标准三维曲面
sphere函数
- 调用格式:
[x, y, z]=sphere(n):这个函数将产生三个n+1阶的方阵。 - 参数解释:采用这三个方阵可以直接绘制出,圆心位于原点,半径为一的单位球体。若在调用该函数时,不带输出参数,将直接绘制球面。参数n决定了球面的圆滑程度。默认值是20,若n较小,则将绘制出多面体表面图
- 调用格式:
cylinder函数:
调用格式:
[x, y, z]=cylinder(R,n)参数解释:R是一个向量,存放柱面各个等间隔高度上的半径。n表示在圆柱圆周上有n个间隔点,默认为20。如果n是一个标量,则生成一个柱面
示例:
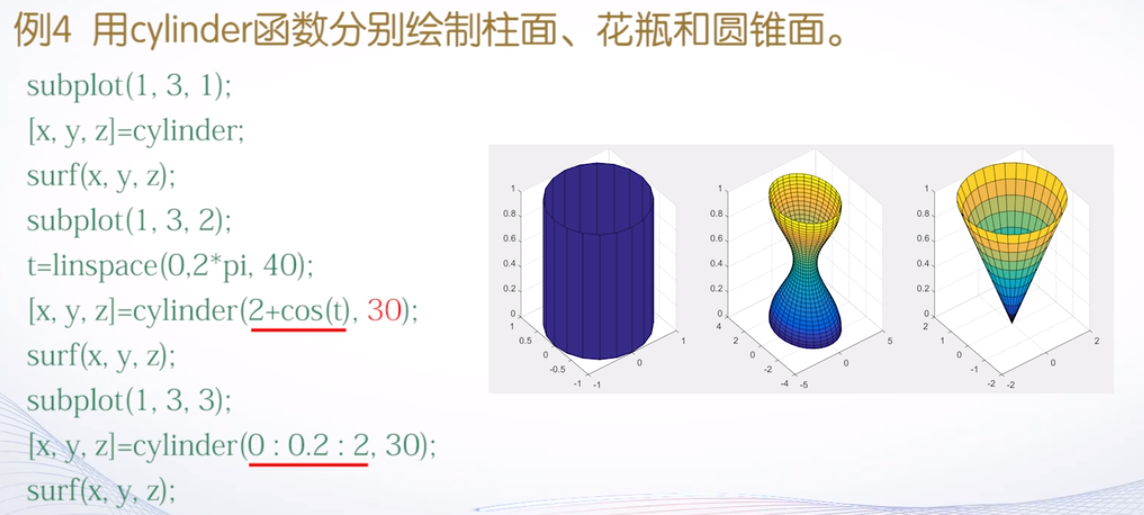
* <img src="https://raw.githubusercontent.com/readLemon/mdPic/Manjaro/matlab.md/cylinder2.png" alt="cylinder2" style="zoom:50%;" />- peaks函数
fmesh函数和fsurf函数
适用于图形有三个参数方程,并且有两个自变量定义。
fmesh
- 调用格式:
fsurf(funx, funy, funz, uvlims)
- 调用格式:
fsurf
- 调用格式:
fmesh(funx, funy, funz, uvlims)
- 调用格式:
参数解释:其中,funx、funy、funz代表定义曲面x、y、z坐标的函数,通常采用函数句柄的形式。nvlims为funx、funy、funz的自变量的取值范围,采用4元向量[umin, umax, vmin, vmax]描述。默认为[-5, 5, -5, 5]
示例,一个画的上半段曲面,一个下半段

图形修饰处理
视点处理
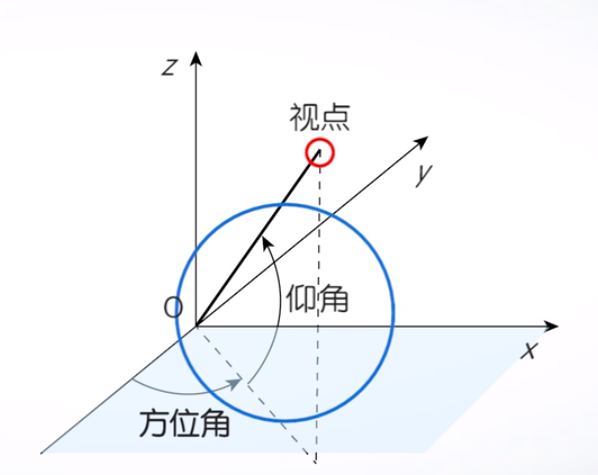
方位角和仰角
view函数
调用格式:
view(az, el):其中az为方位角,el为仰角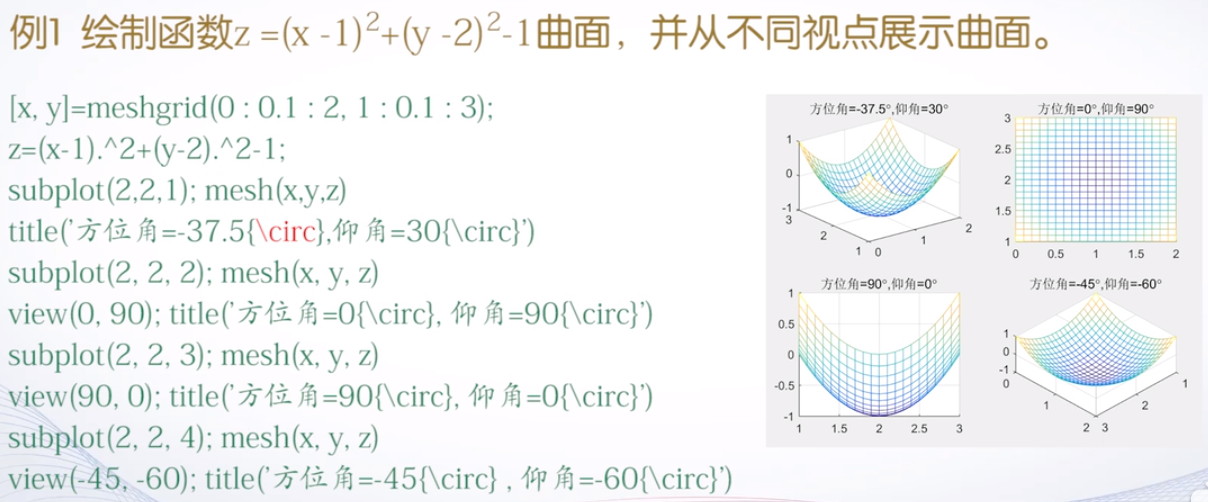
其他调用格式
view(x, y, z):x、y、z为视点在迪卡尔坐标系中的位置view(2):从二维平面观察图形,即方位角为零度,仰角为90度view(3):从三维空间观察视图,视点为默认方位角和仰角
色彩处理
颜色的向量表示
- [0 0 1]:蓝色
- [1 0 0]:红色
- [0 1 0]:绿色
- [1 1 1]:白色
- [0 0 0]:黑色
- …..
色图
色图矩阵
内建色图

指定当前图形使用的色图
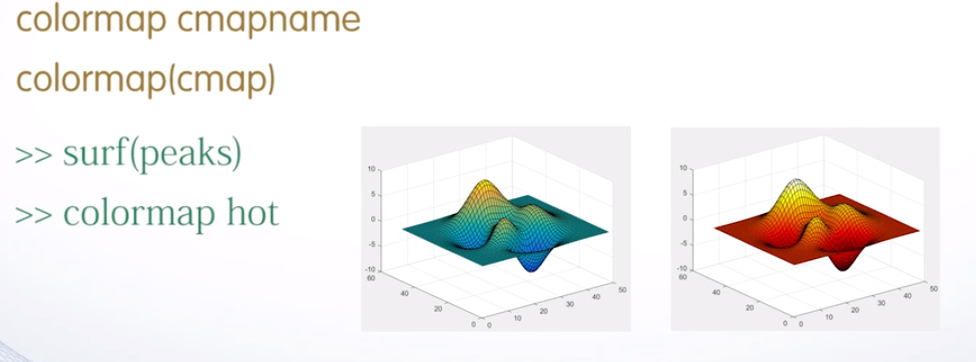
创建色图矩阵:色图矩阵的每一行是RGB三元组。可以自定义色图矩阵,也可以调用MATLAB提供的函数来自定义色图矩阵

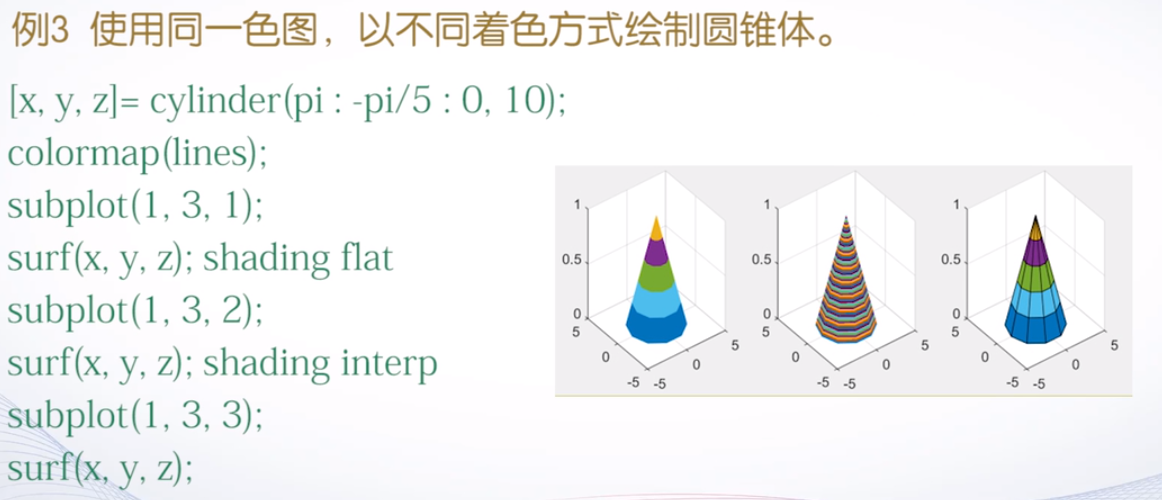
三维图形表面的着色:MATLAB由自定义的着色方式,但是也可以自己自定义着色方案
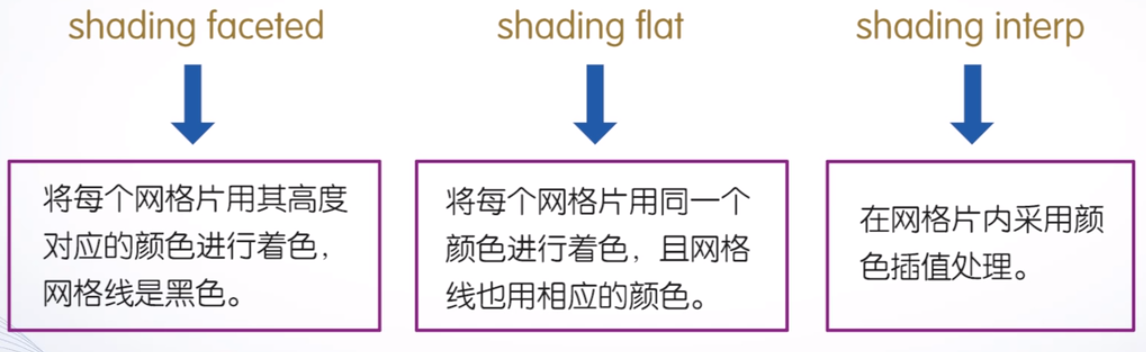
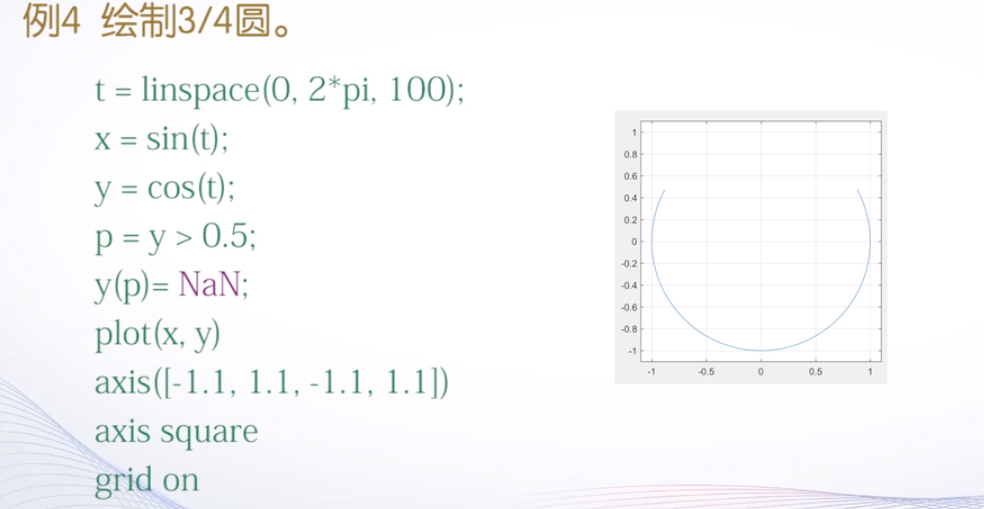
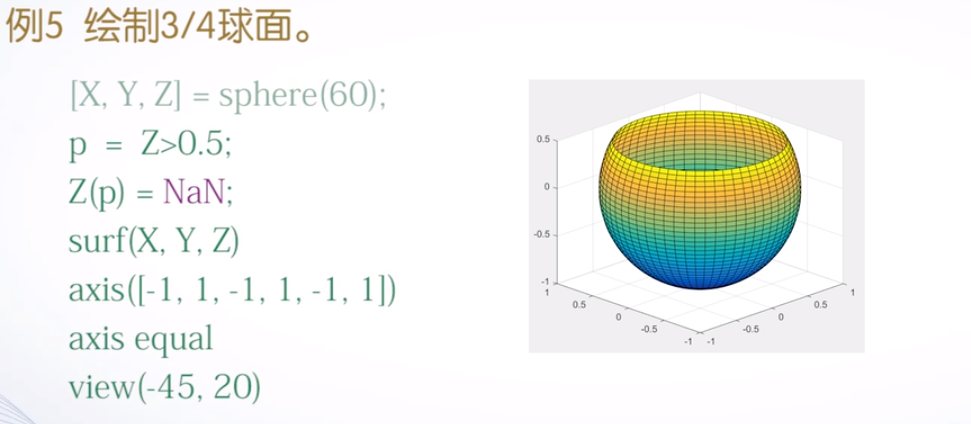
剪裁处理
将图形中需要剪裁部分对应的函数值设置成NaN,这样在绘制图形时,函数值为NaN的部分将不显示出来,从而达到对图形进行剪裁的目的
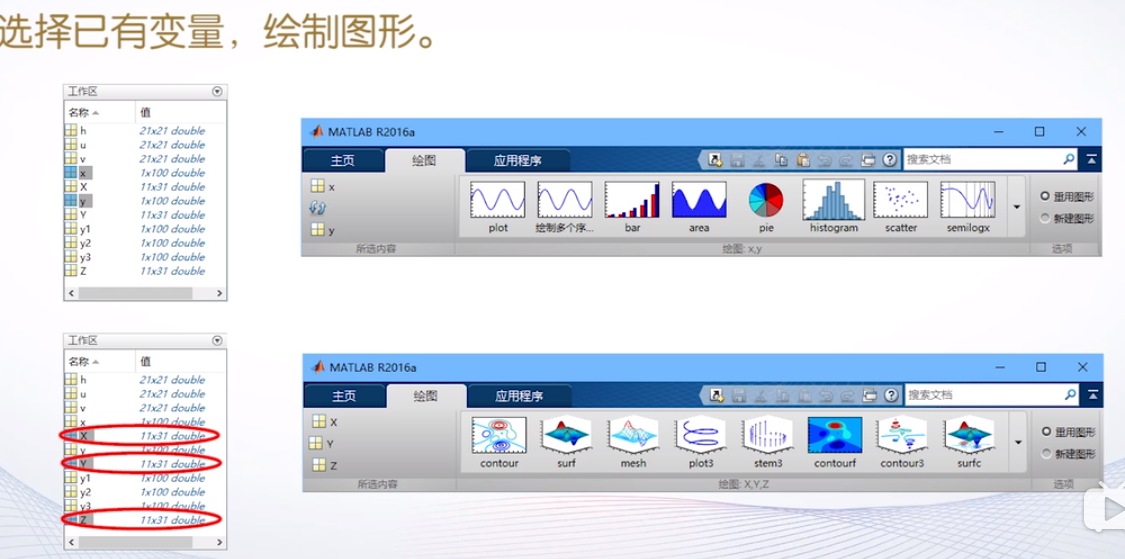
交互式绘图工具
”绘图“选项卡
图形窗口绘图工具
ps:默认不显示,需要手动打开
- 显示
- ”显示绘图工具和停靠图形“按钮
- 在命令行中输入
plottools
- 绘图工具的组成
- 图形选项板
- 新子图面板
- 变量面板
- 注释面板
- 绘图浏览器:选中一个图例后,其周围会有方格点,可以选中坐标轴点击下方添加数据在该图中添加新图型
- 属性编辑器
- 曲线属性编辑器
- 坐标系属性编辑器
- 图形窗口属性编辑器
- 图形选项板
图形窗口菜单和工具栏
数据分析与多项式计算
数据统计分析
求最大元素与最小元素
max():求向量或矩阵的最大元素。- 当参数为向量时,有两种调用格式
y=max(x):返回向量的最大值,如果x包含复数元素,则按模取最大值[y,k]=max(x):返回x中的最大值存入y,最大值与元素的序号存入k,如果x中包含复数,则按模取最大值
- 当参数为矩阵时,函数由三种调用格式
max(A):返回一个行向量,向量的第i个元素是矩阵A的第i列上的最大值[Y,U]max(A):返回行向量Y和U,Y记录A的每列的最大值,U向量记录每列最大值元素的行号max(A,[],dim):dim取1或者2。dim取1时,该函数的功能和max(A)完全相同; dim取2时,函数返回一个列向量,其第i个元素是矩阵A的第i行上的最大值
- 当参数为向量时,有两种调用格式
min():求向量或矩阵的最小元素(用法与max类似)
求平均值与中值
这两个函数和max函数调用相似
mean():求算数平均值median():中值
求和与求积
sum():求和函数prod():求积函数
累加和与累乘积
cumsum(A):累加和函数如果A是一个向量,则累加函数得到的值也是一个和A等长的向量,得到向量相应位置上的值为A中的第一位的值累加到相应位的值。
cumprod(A):累乘积函数与累加函数类似
求标准差与相关系数

std():标准差函数std(x):计算向量x的标准差std(A):计算矩阵A的各列的标准差std(A,flag, dim):flag取0或1。当flag取0时,按S1所列公式计算样本标准差,当flag取1时,按S2所列公式计算总体标准差。在默认情况下,flag=0,dim=1
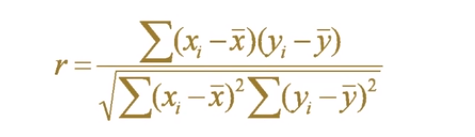
correcoef():相关系数函数- 调用格式1:
corrcoef(A):返回由矩阵A所形成的一个相关系数矩阵,其中,第i行第j列的元素表示原矩阵A中第i列和第j列的相关系数 - 调用格式2:
corrcoef(X,Y):在这里,x、y是向量,他们与corrcoef([X,Y])的作用一样,用于X、Y向量之间的相关系数
- 调用格式1:
- 求出来r处于[-1,1],值越大,说明相关性越高
排序
sort():排序函数- 调用格式:
sort(X):对向量X按升序排列 - 调用格式:
[Y, I]=sort(A,dim,mode):dim指明对A的列还是行进行排序(1列2行)。mode指明按升序还是降序排序,若取“acend”,则按升序。若取“descend”,则按降序,默认升序。输出参数中,Y是排序后的矩阵,而I记录Y中的元素在A中的位置
- 调用格式:
多项式计算
多项式的表示

多项式的四则运算
- 多项式加减运算:相应的向量相加减即可
- 多项式惩罚
- 调用格式:
conv(P1,P2):多项式相乘函数。这里的P1和P2是两个多项式系数向量。返回的结果也是多项式
- 调用格式:
- 多项式除法
- 调用格式:
[Q,r]=deconv(P1,P2):多项式相除函数:其中,Q返回多项式P1除以P2的商式,r返回P1除以P2的余式。这里,Q和r仍是多项式系数向量 deconv是conv的逆函数。因此有P1=conv(Q,P2)+r
- 调用格式:
多项式的求导
polyder()函数- 调用格式1:
p=polyder(P):求多项式P的导函数 - 调用格式2:
p=polyder(P,Q):求PQ乘积的导数 - 调用格式3:
[p,q]=polyder(P,Q):求P/Q的导函数,导函数的分子存入p,分母存入q
- 调用格式1:
多项式的求值
polyval(p,x):代数多项式求值- 其中,p为多项式系数向量,x可以是标量、向量或者矩阵。若x为标量,则求多项式在该点的值,若x为向量或矩阵,则对向量或矩阵中的每个元素求多项式的值
polyvalm(p,x):矩阵多项式求值- 其调用格式与polyval相同,但是含义不同。本函数要求x为方阵,以方阵为自变量求多项式的值
区别:

多项式的求根
roots(p):多项式求根函数- 其中,p为多项式的系数向量
poly(x):x为多项是的全部根。可以用该函数建立其原多项式
数据插值
数据插值的计算机制
数据插值的实现方法
interp1()函数:一维插值函数调用格式:
Y1=interp1(X,Y,X1,method):根据X、Y的值,计算函数在X1处的值。其中X、Y是两个等长的已知向量,分别表示采样点和采样值。X1是一个向量或者标量,表示要插值的点method用于指定插值方法,常用的取值有以下四种
- linear:线性插值,默认方法。将与插值点靠近的两个数据点用直线连接,然后在直线上选取对应插值点的数据
- nearest:最近点插值。选择最近样本点的值作为插值数据
- pchip:分段3次埃尔米特插值。采用分段三次多项式,除满足插值条件,还需满足在若干节点处相邻段插值函数的一阶导数相等,使得曲线光滑的同时,还具有保行性
- spline:三次样条插值。每个分段内构造一个三次多项式,使其插值函数除满足插值条件外,还要求在各节点处具有连续的一阶和二阶导数
- 拉格朗日插值
- 牛顿插值
- …
interp2()函数:二维插值函数- 调用格式:
interp2(X,Y,Z,X1,Y1,method):其中X、Y是两个向量,表示两个参数的采样点,Z是采样点对应的函数值。X1、Y1是两个标量或向量,表示要插值的点 - method如上
- 调用格式:
数据拟合
polyfit():多项式拟合函数。可以求得最小二乘拟合多项式系数- 调用格式1:
P=polyfit(X,Ym) - 调用格式2:
[P,S]=polyfit(X,Y,m) - 调用格式3:
[P,S,mu]=polyfit(X,Y,m):根据样本数据X和Y,产生一个m次多项式p及其在采样点误差数据S,mu是一个二元向量,mu(1)是mean(X),二mu(2)是std(X)
- 调用格式1:
polyval(p,v):计算多项式在指定位置的值。p是多项式系数矩阵,v是未知数的值
数值微积分与方程组求解
数值微分方程与数值积分
线性方程组求解
非线性方程求解与函数极值计算
常微分方程数值求解
初体验
Simulink系统仿真
Simulink仿真基础
Simulink的启动
- 启动方式1:在MATLAB主窗口选择“主页”选项卡,再单击“文件”命令组件中的“新建”命令按钮,然后从下拉菜单中选择“SImulink Model”命令
- 在“主页”选项卡中单击“SIMULINK”命令组中的“Simulink”命令按钮
- 在命令窗口中输入
simulink命令 - 建立好新窗口以后
- 单击“Library Browser”按钮,将打开Simulink模块库浏览器窗口,此时,可以通过鼠标将模块库中的模块拖动到模型编辑窗口,在将各个模块连接起来,就构成了仿真模型
系统仿真模型的创建
- Simulink模块的操作
- 模块的添加:在模块库中找到该模块,然后直接拖到模型编辑窗口中即可
- 模块的删除
- 模块的连接
- 连线的分支:把鼠标放在连好的线上,按下Ctrl,在拖拽即可
仿真参数的设置
- 模块参数设置
- 方法1:双击要设置的模块
- 方法2:选择要设置的模块,再选择Diagram –>Block Parameters命令
- 方法3:右击要设置的模块,从快捷菜单中选择Block Parameters命令
- 仿真参数设置
- 打开
- 选择Simulation –>Model Configuration Parameters命令
- 单击工具栏中的Model Configuration Parameters命令按钮
- Solver selection
- Type:分为固定步长和变步长
- Solver:具体算法
- 打开
子系统的创建与封装
子模块建立
通过Subsystem模块建立子系统:拖入一个Subsystem模块,然后点进去编辑
将已有的模块转换为子系统
选中子模型的所有模块,然后菜单Diagram –> Subsystem&Model Reference –>Creat Subsystem from Selection
也可以用Ctrl+G
子系统的封装
- 选中子系统 –>Diagram –>Mask –>Creat Mask…
- 第一个选项卡用于设置被封装的图标
- 第二个选项卡用于设置子系统设置对话框
- 第三个选项卡用于设置初始化命令
- 第四个选项卡用于定义封装模块的类型、描述和帮助文本
子系统的条件执行
使能子系统
触发子系统
可直接选择Triggered Subsystem模块,或展开已有子系统,添加Ports&Subsystems模块库中的Trigger模块,将本模块转化为出发子系统
触法形式
- rising:上跳沿触发
- falling:下跳沿触发
- either:上跳沿或下跳沿触发
- function-call:函数调用触法。必须与S函数配合
使能触发子系统
S函数的设计与应用
S函数是系统函数的简称,是指采用一种程序设计语言描述的一个功能模块
用户可以采用MATKAB语言,也可以采用C、C++或FORTRAN等语言来编写S函数
S函数有自己特定的语法构成规则,可以用来描述并实现连续系统、离散系统以及复合系统
S函数能够接收来自Simulink求解算法的相关信息,并对求解算法发出的命令做出适当的响应,这种交互作用类似于Simulink系统模块与求解算法的相互作用
MATLAB文件操作
文件的打开与关闭
fopen()函数:用于打开文件- 调用格式:
fid=fopen(filename,permission):其中fid为文件识别号,filename为待操作文件名。permisson为对文件的允许使用的方式。文件不存在时,fid为-1r:以只读打开一个文件w:以写的方式打开一个文件,如果文件不存在,则新建一个,再打开a:表示在文件末尾添加数据r+:以读和写的方式打开一个文件
- 调用格式:
fclose():用于关闭已打开的文件- 调用格式:
status=fclose(fid):fid为文件识别号,如果fid为all,则关闭所有已经打开的文件
- 调用格式:
文本文件的读写
fscanf函数和fprintf函数:fscanf函数用于读取文本的内容,fprintf用于将数据写入文本中。- 调用格式:
[A,count]=fscanf(fid,fmt,size)、count=fprintf(fid,fmt,A):其中,A用于存放读写的数据,count返回成功读写的数据元素的个数;参数fid为文件标识号,fmt用以控制读取的数据格式,size用于指定A的大小
- 调用格式:
数据文件定位
单变量线性函数
使用plot函数画图查看
使用fzero函数
已经事先知道根在x = 0.5和x = 2.5附近

符号求根函数
solve
1
2
3syms x #定义一个符号x
X = solve(x^2-3*x+1) #调用solve函数求根
X = eval(X) #通过eval函数将符号解转换成数字解使用工具箱中的函数
fsolve其第三个参数用于设置优化参数,这里的 Display off表示不显示中间的迭代结果
